Multithreaded: Addition mit einer geteilten Variable

Ziel dieses Artikels ist es, die Summe aller Elemente eines Vektors zu bilden. Habe ich es im letzten Artikel mit einem Thread versucht, nütze ich dieses mal die volle Power meiner PCs. Ich verwende eine gemeinsame Summen-Variable, die von allen Threads gleichzeitig benutzt wird. Was bei ersten Hinsehen wie eine gute Idee klingt, ist bei genauerem Blick eine sehr naive Strategie. Überwiegt der Aufwand für die Synchronisation der Summen-Variable deutlich den Performanzvorteil der vier bzw. zwei CPUs.

Die Strategie

In Anlehnung an meinen letzten Artikel berechne ich die Summe von 100 000 000 Millionen Zufallszahlen zwischen 1 und 10. Um mich einfach zu vergewissern, dass alle Ergebnisse richtig berechnet werden, schränke ich den Zufall ein. So setze ich dieses Mal keinen seed ein, so dass immer die gleichen Zufallszahlen auf meinen zwei Architekturen erzeugt werden. Daher ist es einfach zu sehen, dass die Programme das gewünschte Ergebnis liefern. Beide Programme lasse ich auf einer 4 CPU Maschine unter Linux und einer 2 CPU Maschine unter Windows laufen. In bekannter Tradition mit maximaler und ohne Optimierung. Insbesondere auf Windows haben mich die Ergebnisse sehr verwirrt.

Welche Fragen interessieren mich in diesem Artikel?

Wie unterscheidet sich die Performanz eines Locks gegenüber der einer atomaren Variable?
Wie schneiden die hier vorgestellten Ergebnisse im Vergleich zu der Single-Threaded Lösung mit std::accumulate im letzten Artikel ab?

Schutz der gemeinsamen Variable mit std::lock_guard

Die einfachste Art, eine von Threads geteilte Variable zu schützen, ist ein Mutex verpackt in einem Lock.

// synchronizationWithLock.cpp

#include <chrono>
#include <iostream>
#include <mutex>
#include <random>
#include <thread>
#include <utility>
#include <vector>

constexpr long long size= 100000000;   

constexpr long long firBound=  25000000;
constexpr long long secBound=  50000000;
constexpr long long thiBound=  75000000;
constexpr long long fouBound= 100000000;

std::mutex myMutex;

void sumUp(unsigned long long& sum, const std::vector<int>& val, unsigned long long beg, unsigned long long end){
    for (auto it= beg; it < end; ++it){
        std::lock_guard<std::mutex> myLock(myMutex);
        sum+= val[it];
    }
}

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  std::mt19937 engine;
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));
 
  unsigned long long sum= 0;
  auto start = std::chrono::system_clock::now();
  
  std::thread t1(sumUp,std::ref(sum),std::ref(randValues),0,firBound);
  std::thread t2(sumUp,std::ref(sum),std::ref(randValues),firBound,secBound);
  std::thread t3(sumUp,std::ref(sum),std::ref(randValues),secBound,thiBound);
  std::thread t4(sumUp,std::ref(sum),std::ref(randValues),thiBound,fouBound);   
  
 
  t1.join();
  t2.join();
  t3.join();
  t4.join();
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << sum << std::endl;

  std::cout << std::endl;

}

Das Programm ist schnell skizziert. Die Funktion sumUp (Zeile 20 - 25) beschreibt das Arbeitspaket, das jeder Thread zu erledigen hat. Dieses erhält die Summen-Variable sum und den std::vector val per Referenz als Parameter. beg und end begrenzen den Bereich des Vektors, von dem die Funktion die Summe bildet. Damit der Zugriff auf die gemeinsame Variable geschützt ist, locke ich diese mit einem std::lock_guard (Zeile 22). Jeder Thread in Zeile 41 - 44 berechnet ein Viertel der Summe.

Nun fehlt nur noch die Ausgabe des Programms.

Ohne Optimierung

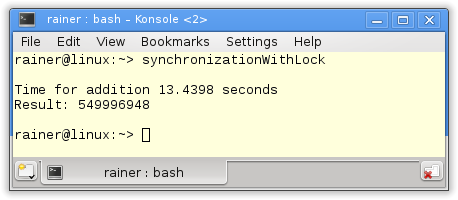
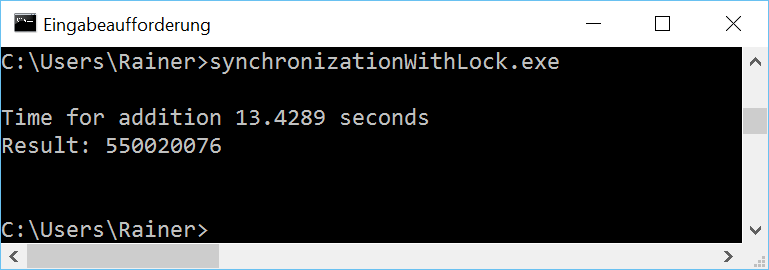
synchronizeWithLock synchronizeWithLock win

Mit maximaler Optimierung

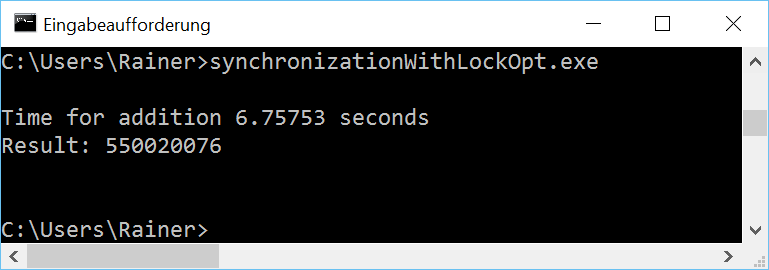
synchronizeWithLockOpt synchronizeWithLockOpt win

Der Flaschenhals des Programms ist die gemeinsame Variable, die aufwändig durch ein std::lock_guard geschützt werden muss. Daher besteht die naheliegende Verbesserung des Programms darin, das schwergewichtige Lock durch eine leichtgewichtige atomare Variable zu ersetzen.

Addition mit einen atomaren Variable

Nun ist sum eine atomare Variable. Sonst ändert sich kaum etwas am Programm. Der std::lock_guard ist in der Funkton sumUp (Zeile 18 -22) überflüssig.

// synchronizationWithAtomic.cpp

#include <atomic>
#include <chrono>
#include <iostream>
#include <random>
#include <thread>
#include <utility>
#include <vector>

constexpr long long size= 100000000;   

constexpr long long firBound=  25000000;
constexpr long long secBound=  50000000;
constexpr long long thiBound=  75000000;
constexpr long long fouBound= 100000000;

void sumUp(std::atomic<unsigned long long>& sum, const std::vector<int>& val, unsigned long long beg, unsigned long long end){
    for (auto it= beg; it < end; ++it){
        sum+= val[it];
    }
}

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  std::mt19937 engine;
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));
 
  std::atomic<unsigned long long> sum(0);
  auto start = std::chrono::system_clock::now();
  
  std::thread t1(sumUp,std::ref(sum),std::ref(randValues),0,firBound);
  std::thread t2(sumUp,std::ref(sum),std::ref(randValues),firBound,secBound);
  std::thread t3(sumUp,std::ref(sum),std::ref(randValues),secBound,thiBound);
  std::thread t4(sumUp,std::ref(sum),std::ref(randValues),thiBound,fouBound);   
  
 
  t1.join();
  t2.join();
  t3.join();
  t4.join();
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << sum << std::endl;

  std::cout << std::endl;

}

Ohne Optimierung

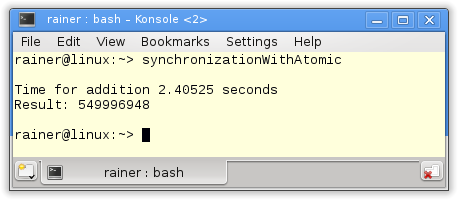
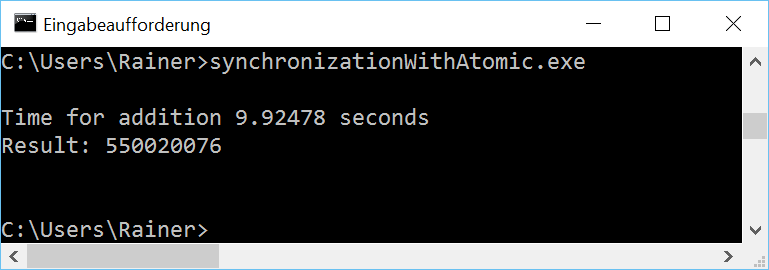
synchronizeWithAtomic synchronizeWithAtomic win

Mit maximaler Optimierung

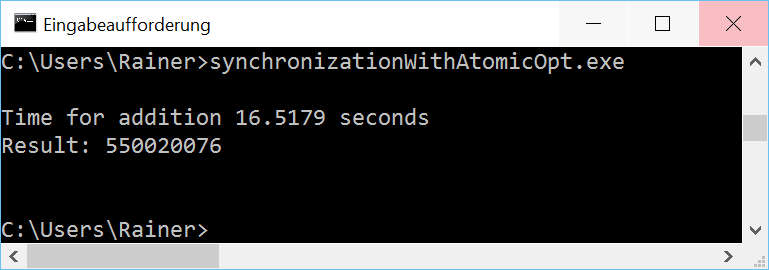
synchronizeWithAtomicOpt synchronizeWithAtomicOpt win

Ein seltsames Phänomen

Wer die Beispiele genau studiert, wird mit Verwunderung feststellen, dass unter Windows das maximal optimierte Programm langsamer ist als das nicht optimierte. Dieses Phänomen hat sich bei den zwei folgenden Variationen von atomaren Variablen bestätigt. Das hat mein Verständnis von Optimierung auf den Kopf gestellt. Daher habe ich die Programme zusätzlich auf einem virtualisierten Windows 8 mit nur einer CPU laufen lassen. Auf diesem war die optimierte Variante aber schneller. Irgendetwas scheint auf Windows 10 mit atomaren Variablen noch nicht rund zu laufen.

Neben += kann der Wert einer atomaren Variable auch mit fetch_add verändert werden. Erwartungsgemäß sollten beide Varianten ein sehr ähnliches Zeitverhalten besitzen.

Addition mit fetch_add

Die Variante mit fetch_add unterscheidet sich kaum von der vorherigen Variante. Lediglich die Zeile 20 ändert sich.

// synchronizationWithFetchAdd.cpp

#include <atomic>
#include <chrono>
#include <iostream>
#include <random>
#include <thread>
#include <utility>
#include <vector>

constexpr long long size= 100000000;   

constexpr long long firBound=  25000000;
constexpr long long secBound=  50000000;
constexpr long long thiBound=  75000000;
constexpr long long fouBound= 100000000;

void sumUp(std::atomic<unsigned long long>& sum, const std::vector<int>& val, unsigned long long beg, unsigned long long end){
    for (auto it= beg; it < end; ++it){
		sum.fetch_add(val[it]);
    }
}

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  std::mt19937 engine;
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));
 
  std::atomic<unsigned long long> sum(0);
  auto start = std::chrono::system_clock::now();
  
  std::thread t1(sumUp,std::ref(sum),std::ref(randValues),0,firBound);
  std::thread t2(sumUp,std::ref(sum),std::ref(randValues),firBound,secBound);
  std::thread t3(sumUp,std::ref(sum),std::ref(randValues),secBound,thiBound);
  std::thread t4(sumUp,std::ref(sum),std::ref(randValues),thiBound,fouBound);   
  
 
  t1.join();
  t2.join();
  t3.join();
  t4.join();
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << sum << std::endl;

  std::cout << std::endl;

}

Ohne Optimierung

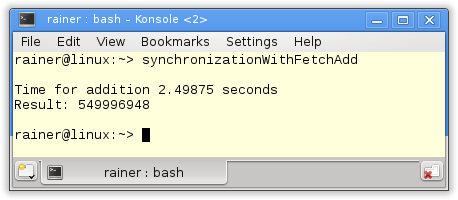
synchronizeWithFetchAdd

Mit maximaler Optimierung

synchronizeWithFetchAddOpt synchronizeWithFetchAddOpt win

Genau genommen stellt die fetch_add Variante kein Fortschritt gegenüber der += Variante dar, bei der die Werte sehr intuitiv addiert werden können. Es gibt aber doch einen feinen Unterschied.

Addition mit fetch_add und Relaxed-Semantik

Das Default-Verhalten für atomare Operationen ist die Sequentielle Konsistenz. Dies gilt für die Addition und Zuweisung auf einer atomaren Variable mit +=, dies gilt auch für die fetch_add Variante. Darüber hinaus lässt sich für fetch_add wie mit allen fetch-Variationen das Speichermodell explizit angeben. Dieses Optimierungspotential nütze ich in dem Beispiel in Zeile 20.

// synchronizationWithFetchAddRelaxed.cpp

#include <atomic>
#include <chrono>
#include <iostream>
#include <random>
#include <thread>
#include <utility>
#include <vector>

constexpr long long size= 100000000;   

constexpr long long firBound=  25000000;
constexpr long long secBound=  50000000;
constexpr long long thiBound=  75000000;
constexpr long long fouBound= 100000000;

void sumUp(std::atomic<unsigned long long>& sum, const std::vector<int>& val, unsigned long long beg, unsigned long long end){
    for (auto it= beg; it < end; ++it){
		sum.fetch_add(val[it],std::memory_order_relaxed);
    }
}

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  std::mt19937 engine;
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));
 
  std::atomic<unsigned long long> sum(0);
  auto start = std::chrono::system_clock::now();
  
  std::thread t1(sumUp,std::ref(sum),std::ref(randValues),0,firBound);
  std::thread t2(sumUp,std::ref(sum),std::ref(randValues),firBound,secBound);
  std::thread t3(sumUp,std::ref(sum),std::ref(randValues),secBound,thiBound);
  std::thread t4(sumUp,std::ref(sum),std::ref(randValues),thiBound,fouBound);   
  
 
  t1.join();
  t2.join();
  t3.join();
  t4.join();
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << sum << std::endl;

  std::cout << std::endl;

}

Warum kann ich in dem Beispiel die Relaxed-Semantik in Zeile 20 verwenden? Sichert die Relaxed-Semantik doch nicht zu, dass ein Thread die Operationen eines anderen Threads in der gleichen Reihenfolge sieht. Diese Zusicherung ist bei der Addition nicht notwendig. Entscheidend ist nur, dass die Additionen atomar ausgeführt werden.

Schlägt sich meine letzte Optimierung auch im Zeitverhalten der Programme nieder?

Ohne Optimierung

synchronizeWithFetchAddRelaxed

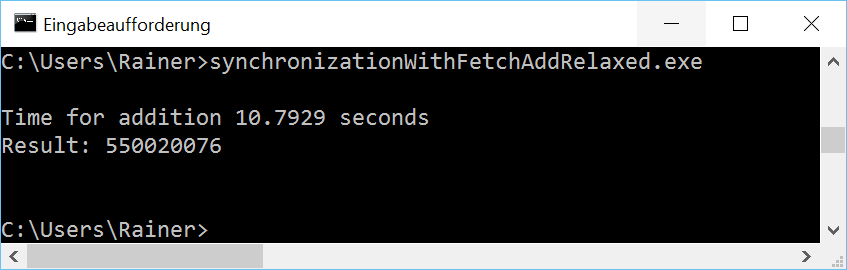
Mit maximaler Optimierung

synchronizeWithFetchAddRelaxedOpt

Linux mit dem GCC ist mit der Operation fetch_add und der Relaxed-Semantik am schnellsten. Die Ergebnisse unter Windows kann ich nicht nachvollziehen.

Zum Abschluss wieder alle Zahlen im Überblick.

Der Überblick

Zwar habe ich sukzessive den Zugriff auf die gemeinsame Variable optimiert und ein immer schnelleres Programm erzeugt. Die Ergebnisse sind aber ernüchternd. Die Addition im Single-Threaded Fall mit std::accumulate schlägt meine Optimierung mit einer gemeinsamen Variablen um Welten. Genau genommen mindestens um den Faktor 40.

MultithraedeSharedVariable

Wie geht's weiter?

Im nächsten Artikel werde ich das beste aus beiden Welten kombinieren. In dem Artikel kombiniere ich die nicht synchronisierte Addition in einem Thread mit der Power von mehreren Threads. Mal schauen, ob ich damit die Performanz der Single-Threaded Variante mit std::accumulate schlage.

title page small Go to Leanpub/cpplibrary "What every professional C++ programmer should know about the C++ standard library". Hole dir dein E-Book. Unterstütze meinen Blog.