CppMem ist das Werkzeug, um kleine Multithreading-Programme zu analysieren. Daher will ich in diesem Artikel bewusst einfach starten.

In der Miniserie dieses Blocks Sukzessive Optimierung habe ich in einem kleinen Spiel das verschränkte Lesen und Schreiben auf verschiedenen Threads optimiert. Nicht immer waren die Programme wohldefiniert. Dieses Spiel werde ich jetzt nochmals durchspielen. Dieses Mal soll mir aber CppMem bei meiner Analyse helfen.

Zuerst aber der Ausgangsprogramm.

Das Programm

Das Original

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

// readWriteUnsynchronized.cpp

#include <iostream>
#include <thread>

int x= 0;
int y= 0;

void writing(){
  x= 2000;
  y= 11;
}

void reading(){ 
  std::cout << "y: " << y << " ";
  std::cout << "x: " << x << std::endl;
}

int main(){
  std::thread thread1(writing);
  std::thread thread2(reading);
  thread1.join();
  thread2.join();
};

Ich fasse nur kurz das Ergebnis der Programmausführung zusammen. Das Programm besitzt undefiniertes Verhalten, da die Lese- und Schreibe-Operationen auf nicht atomaren Variablen nicht synchronisiert stattfinden. Es ist damit keine Aussage zur Ausgabe von x und y möglich.

Die genauere Analyse gibt es natürlich in dem Artikel Sukzessive Optimierung oder in ein paar Zeilen mit CppMem. Das Schreiben eines Multithreading-Programms ist mit CppMem deutlich einfacher.

CppMem

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

int main() {
  int x=0; 
  int y=0;
  {{{ { 
        x= 2000; 
        y= 11;
      }
  ||| {
        y;
        x;
      }  
  }}}
}

Das Programm ist auf das Wesentliche reduziert. Durch die drei geschweiften Klammern (Zeile 4 und 12) bzw. die Pipe-Symbole (Zeile 8) definiere ich einen Thread. Die zusätzlichen geschweiften Klammern im Thread (Zeile 4 und 7, bzw. Zeile 8 und 11) definieren das Arbeitspaket des Threads. Da ich nicht an der Ausgabe der Variable x und y interessiert bin, lese ich deren Werte nur in der Zeile 9 und 10.

Das war schon fast die ganze Theorie. Jetzt werde ich das Programm mit CppMem analysieren.

Die Analyse

Führe ich das Programm aus, moniert CppMem in roten Buchstaben (1), das alle vier Programmausführungen nicht race free sind. Eine Ausführung ist konsistent. Zwischen diese 4 Ausführungen kann ich nun in (2) hin und her wechseln und den jeweiligen annotierten Graph (3) analysieren.

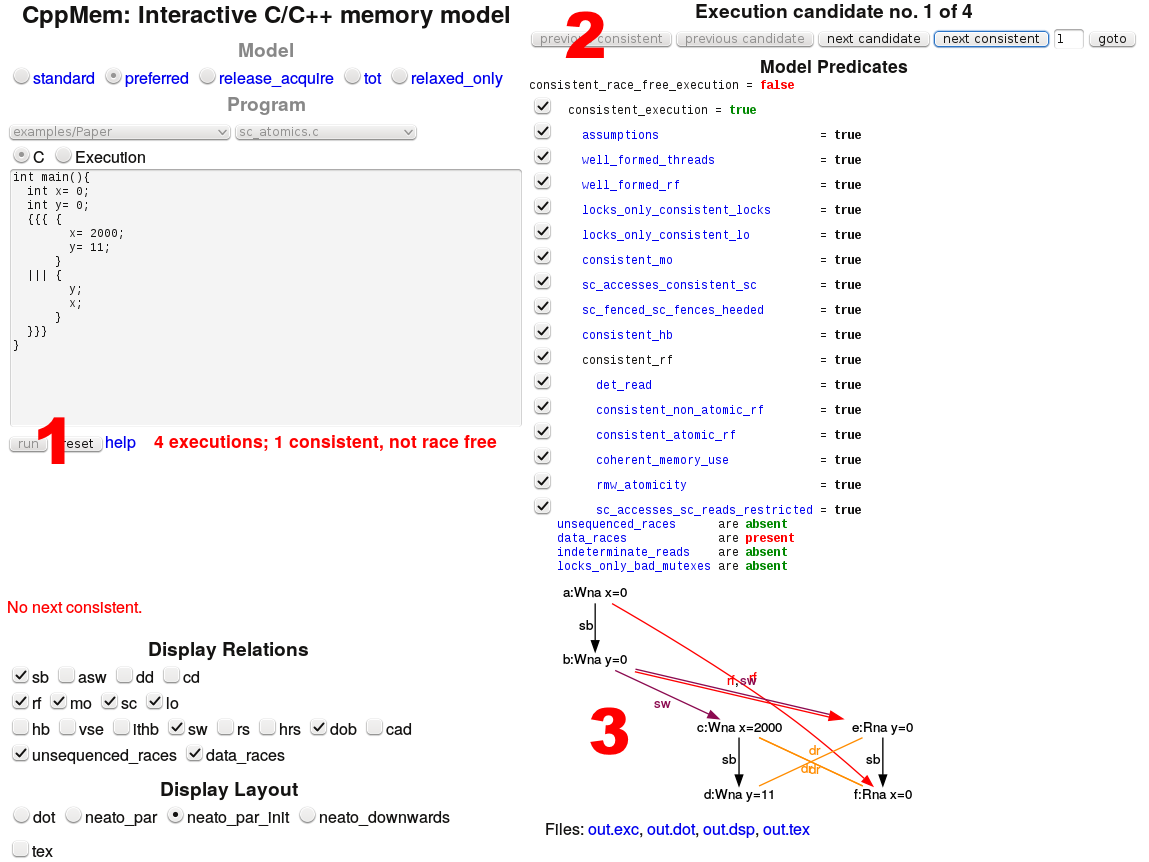
Der meiste Informationsgehalt steckt im Graph. Daher werde ich mir die vier Graphen genauer anschauen.

Erste Ausführung

Was lässt sich aus dem Graph (3) ablesen?

Die Knoten des Graphen repräsentieren die Ausdrücke des Programms, die Kanten die Beziehungen zwischen den Ausdrücken. Ich werde mich in meiner Erläuterung auf die Namen den Knoten (a) bis (f) beziehen. Was lässt sich aus den Annotationen in dieser konkreten Ausführung ableiten?

• a:Wna x=0: Ist der erste Ausdruck (a), der ein nicht-atomares Schreiben von x darstellt.
• sb (sequenced-before): Das Schreiben des ersten Ausdrucks (a) erfolgt vor dem Schreiben des zweiten Ausdrucks (b). Diese Beziehung gilt auch zwischen den Ausdrücken (c) und (d), bzw. (e) und (f).
• rf (read from): Der Ausdruck (e) liest den Wert für y von dem Ausdruck (b). Entsprechend liest in dieser konkreten Ausführung (f) von (a).
• sw s(synchronizes-with): Der Ausdruck (a) synchronizes-with (f). Diese Beziehung gilt, da der Ausdruck (f) in einem eigenen Thread stattfindet. Die Erzeugung von Threads ist ein Synchronisationspunkt. Alle Aktionen, die vor der Erzeugung eines Threads stattgefunden haben, sind in diesem Thread sichtbar. In Analogie gilt die gleiche Beziehung zwischen (b) und (e).
• dr (data race): Hier ist der kritische Wettlauf zwischen dem Lesen und Schreiben der Variable x und y. Dadurch besitzt das Programm undefiniertes Verhalten.

Warum ist eine Programmausführung konsistent?

Konsistent ist sie, da die Werte x und y von den Werten für x und y im main-Thread (a) und (b) gelesen werden. Werden die Werte hingegen von den Variablen x und y aus dem separaten Thread in den Ausdrücken (c) und (d) gelesen, tritt das Phänomen auf, dass die Werte von x und y in (e) und (f) eventuell nur teilweise gelesen werden können. Das ist nicht konsistent. Oder anders ausgedrückt. In der konkreten Ausführung enthalten die Werte von x und y jeweils den Wert 0. Das zeigt auch der Ausdruck (e) und (f).

Diese Garantie gilt nicht für die drei weiteren Ausführungen, auf die ich noch kurz eingehe.

Zweite Ausführung

In dieser nicht-konsistenten Ausführung liest der Ausdruck (e) den Wert für y von dem Ausdruck (d). Das Schreiben von (d) wird gleichzeitig wie das Lesen von (e) ausgeführt.

Dritte Ausführung

Symmetrische zur zweiten Ausführung, liest der Ausdruck (f) seinen Wert vom Ausdruck (c).

Vierte Ausführung

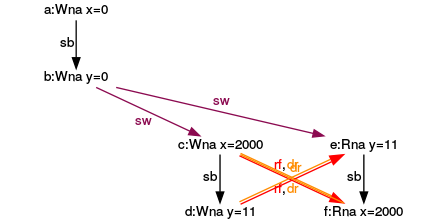
In der letzten Ausführung lesen sowohl der Ausdrücke (e) als auch (f), ihre Werte von den Ausdrücken (d) bzw. (c).

Ein kleines Fazit

Obwohl ich nur die Defaulteinstellung von CppMem verwendet und lediglich die Graphen analysiert habe, liefert mir das Werkzeug schon sehr viel wertvolle Information. Insbesondere bringt CppMem mehrere Aspekte deutlich auf den Punkt:

1. Alle vier Kombinationsmöglichkeiten von x und y sind möglich: (0,0), (11,0), (0,2000), (11,2000).
2. Das Programm besitzt einen kritischen Wettlauf und damit ist die Programmausführung undefiniert.
3. Nur eine der vier Programmausführungen ist konsistent.

Wie geht's weiter?

Weiter geht es mit der Suzessiven Optimierung im nächsten Artikel. Ich bin schon neugierig, welche tiefen Einsichten CppMem liefert.

Go to Leanpub/cpplibrary "What every professional C++ programmer should know about the C++ standard library".   Hole dir dein E-Book. Unterstütze meinen Blog.