In dem Artikel Statisch geprüft habe ich die Funktionalität der Type-Traits Bibliothek als ideale Erweiterung für static_assert vorgestellt. Benötigt doch der Operator static_assert eine Funktion, die zur Compilezeit ihre Entscheidung fällt. Den Beweis bin ich bisher schuldig geblieben. Der Beweis folgt aber jetzt.
ggt - Die Erste
Bevor ich systematisch die Funktionalität der Type-Traits Bibliothek vorstelle, werde ich in diesem Artikel mit einem Beispiel starten. Startpunkt ist der euklidscher Algorithmus zur Berechnung des größten gemeinsamen Teiler(ggT) (greatest common divisor (gcd) ) zweier natürlicher Zahlen.
Schnell habe ich den Algorithmus als Funktions-Template umgesetzt und füttere ihn mit verschiedenen Argumenten.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
// gcd.cpp #include <iostream> template<typename T> T gcd(T a, T b){ if( b == 0 ){ return a; } else{ return gcd(b, a % b); } } int main(){ std::cout << std::endl; std::cout << "gcd(100,10)= " << gcd(100,10) << std::endl; std::cout << "gcd(100,33)= " << gcd(100,33) << std::endl; std::cout << "gcd(100,0)= " << gcd(100,0) << std::endl; std::cout << gcd(3.5,4.0)<< std::endl; std::cout << gcd("100","10") << std::endl; std::cout << gcd(100,10L) << gcd(100,10L) << std::endl; std::cout << std::endl; } |
Das Compilieren des Programms schlägt lautstark fehl. Der Compiler versucht vergeblich die Templates zu instanziieren.
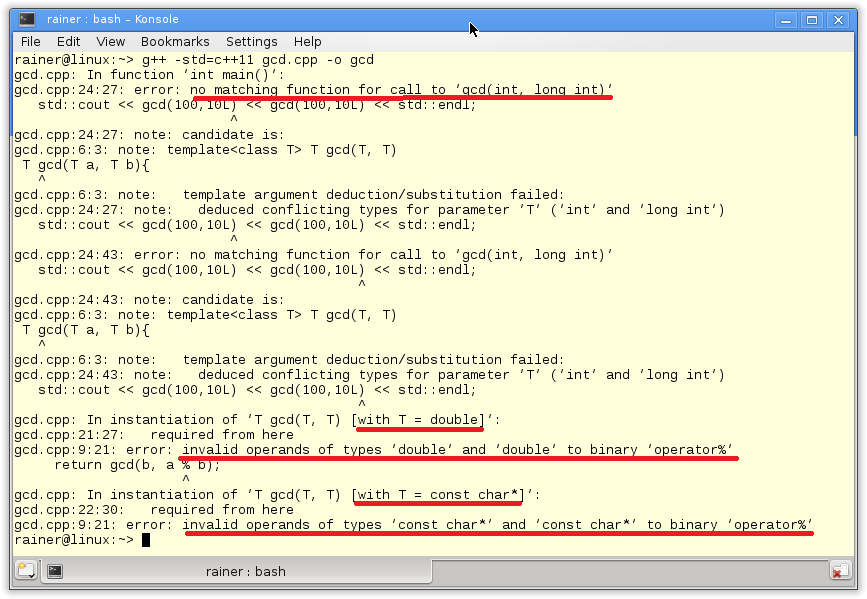
Leider besitzt das Funktions-Template zwei konzeptionelle Probleme. Zum einen ist der gcd-Algorihmus zu generisch. So kann das Funktions-Template double-Werte (Zeile 21) und C-Strings (Zeile 22) als Argumente annehmen. Der größte gemeinsame Teiler auf diesen beiden Datentypen ist nicht definiert. Konkret scheitern die double- und C-String-Werte an dem Modulo-Operator in Zeile 9. Dies ist aber nicht das einzige Problem des Funktions-Templates gcd. gcd hängt von dem Typparameter T ab. Die Signatur (Zeile 6) des Funktions-Templates verrät durch einen scharfen Blick (gcd(T a, T b)), das die Werte a und b vom gleichen Typ sein müssen. Bei Template-Parametern findet keine Konvertierung statt. Das ist der Grund, warum der Aufruf des Funktions-Templates in Zeile 24 mit einem int und einem long-int Typ fehlschlägt.
Das erste Problem ist mit Hilfe der Type-Traits Bibliothek schnell gefixt. Für das Zweite benötige ich einen zweiten, längeren Anlauf.
ggt - Die Zweite
Der Einfachheit halber ignoriere ich in den weiteren Ausführungen, dass die Argumente des Funktions-Templates positive Zahlen sein müssen. Der gcd-Algorithmus fordert, dass seine Argumente natürliche Zahlen sind. Nichts einfacher als das mit der neuen Type-Traits Bibliothek. Mit Hilfe des Operators static_assert und dem Prädikat std::is_integral<T>::value, das zur Compilezeit prüft, ob T ein integraler Typ ist, ist der gcd-Algorithmus schnell verbessert. Ach ja. Ein Prädikat ist eine Funktion, die einen Wahrheitswert zurückgibt.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
// gcd_2.cpp #include <iostream> #include <type_traits> template<typename T> T gcd(T a, T b){ static_assert(std::is_integral<T>::value, "T should be an integral type!"); if( b == 0 ){ return a; } else{ return gcd(b, a % b); } } int main(){ std::cout << std::endl; std::cout << gcd(3.5,4.0)<< std::endl; std::cout << gcd("100","10") << std::endl; std::cout << std::endl; } |
Damit ist das erste konzeptionelle Problem des gcd-Algorithmus elegant gelöst. In dieser Version steigt der Compiler nicht unmotiviert aus, da der Modulo-Operator für einen double-Wert und einen C-String nicht definiert ist, sondern weil er die Zusicherung in Zeile 8 nicht einhalten kann. Der feine Unterschied ist jetzt, dass wir eine eindeutige Fehlermeldung erhalten und keine kryptische Ausgabe einer fehlgeschlagenen Template-Instanziierung, wie im Beispiel 1.

Die Regel ist eigentlich ganz einfach. Der Compiler muss ein fehlerhaftes Programm zurückweisen und eine eindeutige Fehlermeldung zurückgeben.
Nun besteht nur noch das zweite konzeptionelle Problem. Der gcd-Algorithmus soll mit Argumenten verschiedenen Typs umgehen können.
ggt- Die Dritte
Das ist einfach. Doch halt, welchen Rückgabetyp soll das Ergebnis besitzen?
1 2 3 4 5 6 7 8 9 |
template<typename T1, typename T2> ??? gcd(T1 a, T2 b){ static_assert(std::is_integral<T1>::value, "T1 should be an integral type!"); static_assert(std::is_integral<T2>::value, "T2 should be an integral type!"); if( b == 0 ){ return a; } else{ return gcd(b, a % b); } } |
Die drei Fragezeichen in Zeile 2 deuten es an. Soll der Rückgabetyp dem Typ des ersten Arguments oder dem des zweiten Arguments entsprechen? Oder soll er sich nur von den zwei Typen ableiten? Hier kommt die Rettung wieder in Form der Type-Traits Bibliothek. Zwei Variationen stelle ich vor.
Der kleinere Typ
Für den Rückgabetyp der zwei Template-Parameter bietet es sich, den kleineren der beiden Typen zu verwenden. Daher benötigen wir ein Pendant zum ternären Operator zur Compilezeit. Der ternäre Operator kann nur mit Werten, aber nicht mit Typen umgehen. Damit ist der folgende Ausdruck falsch: T=(sizeof(T1) < sizeof(T2))? T1: T2. Die Type-Traits Bibliothek agiert aber auf Typen. Mit std::conditional besitzt sie eine Funktion, die zur Compilezeit einen Ausdruck auswertet und abhängig vom Ergebnis, den ersten oder den zweiten Typ zurückgibt.
Das folgende Programm zeigt die Entscheidung zur Compilezeit.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
// gcd_3_smaller.cpp #include <iostream> #include <type_traits> #include <typeinfo> template<typename T1, typename T2> typename std::conditional <(sizeof(T1) < sizeof(T2)), T1, T2>::type gcd(T1 a, T2 b){ static_assert(std::is_integral<T1>::value, "T1 should be an integral type!"); static_assert(std::is_integral<T2>::value, "T2 should be an integral type!"); if( b == 0 ){ return a; } else{ return gcd(b, a % b); } } int main(){ std::cout << std::endl; std::cout << "gcd(100,10)= " << gcd(100,10) << std::endl; std::cout << "gcd(100,33)= " << gcd(100,33) << std::endl; std::cout << "gcd(100,0)= " << gcd(100,0) << std::endl; std::cout << std::endl; std::cout << "gcd(100,10LL)= " << gcd(100,10LL) << std::endl; std::conditional <(sizeof(100) < sizeof(10LL)), long long, long>::type uglyRes= gcd(100,10LL); auto res= gcd(100,10LL); auto res2= gcd(100LL,10L); std::cout << "typeid(gcd(100,10LL)).name(): " << typeid(res).name() << std::endl; std::cout << "typeid(gcd(100LL,10L)).name(): " << typeid(res2).name() << std::endl; std::cout << std::endl; } |
Die entscheidende Zeile des Programms ist der Rückgabetyp des gcd-Algorithmus in Zeile 8. Da er mit verschiedenen Typen von Template-Argumenten aufgerufen werden kann, kommt er natürlich auch mit gleichen Typen zurecht. Dies zeigen die Zeilen 21 - 24 und die Ausgabe des Programms. Spannender ist da schon die Zeile 27. In ihr wird die Zahl 100 vom Typ int und die Zahl 10 vom Typ long long int verwendet. Das Ergebnis für den größten gemeinsamen Teiler ist die 10. Besonders hässlich ist die Zeile 29. In dieser nimmt die Variable uglyRes vom Typ std::conditional <(sizeof(100) < sizeof(10LL)), long long, long>::type das Ergebnis an. Das geht dank auttomatischer Typableitung mit auto in Zeile 30 und 31 viel leichter von der Hand und ist deutlich weniger fehleranfällig. Schön zeigt der typeid-Aufruf in Zeile 33 und 34, dass der resultierende Typ für Argumente vom Typ int und long long int int ist, dass der resultierende Type für Argumente vom Typ long long int und long int long int ist.

Der gemeinsame Typ
Es geht aber auch ganz anders. Oft ist es notwendig, nicht den kleineren der beiden Typen zu Compilezeit zu bestimmen, sondern einen Typ, zu dem alle Typen implizit konvertiert werden können. Genau das ist die Domäne des Funktions-Templates std::common_type aus der - ich denke du weißt es schon - Type-Traits Bibliothek. std::common_type kann mit beliebig vielen Template-Argumenten umgehen. Formal gesprochen, std::common_type ist ein Variadic Template.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
// gcd_3_common.cpp #include <iostream> #include <type_traits> #include <typeinfo> template<typename T1, typename T2> typename std::common_type<T1, T2>::type gcd(T1 a, T2 b){ static_assert(std::is_integral<T1>::value, "T1 should be an integral type!"); static_assert(std::is_integral<T2>::value, "T2 should be an integral type!"); if( b == 0 ){ return a; } else{ return gcd(b, a % b); } } int main(){ std::cout << std::endl; std::cout << "typeid(gcd(100,10)).name(): " << typeid(gcd(100,10)).name() << std::endl; std::cout << "typeid(gcd(100,10L)).name(): " << typeid(gcd(100,10L)).name() << std::endl; std::cout << "typeid(gcd(100,10LL)).name(): " << typeid(gcd(100,10LL)).name() << std::endl; std::cout << std::endl; } |
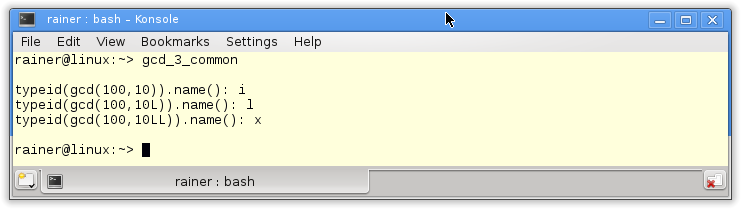
Der einzige Unterschied der letzten Implementierung des gcd-Algorithmus ist es, das std::common_type in Zeile 8 den Rückgabetyp bestimmt. Auf das Ergebnis der Programmausführung habe ich verzichtet. Interessant hingegen sind die Rückgabetypen der Ergebnisse. So ergibt int und int int, int und long int long int und int und long long int long long int.
ggt - Die Vierte
Eine weitere, sehr interessante Variante zu den bisherigen Variationen erlaubt die Funktion std::enable_if aus der Type-Traits Bibliothek. Betrachten wir die bisherigen Implementierung des gcd-Algorithmus, so wird in diesen im Funktionskörper geprüft, ob die Typen natürliche Zahlen sind. Das bedeutet ganz konkret, dass der Compiler immer versucht, den gcd-Algorithmus für seine Funktionsargumente zu instanziieren. Das Ergebnis ist bekannt. Ergibt der Aufruf von std::integral für den Typ false, schlägt die Instanziierung fehl. Das ist nicht optimal. Deutlich optimaler ist es, wenn nur die Funktions-Templates für die Typen zur Verfügung stehen, die die notwendigen Eigenschaften erfüllen. Aus diesem Grund wandert die Zusicherung an das Funktions-Template vom Template-Körper in die Template-Signatur.
Um den Blick aufs Wesentliche zu lenken, sind beide Funktionsargumente vom gleichen Typ sein. Damit ist auch der Typ des Rückgabewerts bereits festgelegt.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
// gcd_4.cpp #include <iostream> #include <type_traits> template<typename T, typename std::enable_if<std::is_integral<T>::value,T>::type= 0> T gcd(T a, T b){ if( b == 0 ){ return a; } else{ return gcd(b, a % b); } } int main(){ std::cout << std::endl; std::cout << "gcd(100,10)= " << gcd(100,10) << std::endl; std::cout << "gcd(3.5,4)= " << gcd(3.5,4.0) << std::endl; std::cout << std::endl; } |
Zeile 7 ist die entscheidende Zeile des Programms. In ihr bestimmt std::is_integral, ob der Type-Parameter T integral ist. Ist T nicht integral, und somit der Rückgabewert der Funktion false, bewirkt dies, dass für diesen Typ keine Templateinstanziierung zur Verfügung steht. Diesen Punkt will ich gerne noch genauer erläutern.
Falls std::enable_if als ersten Parameter true erhält, besitzt std::enable_if ein Mitglied type. Auf dieses Mitglied greift std::enable_if in der Zeile 7 zu. Erhält std::enable_if als ersten Parameter ein false, besitzt es kein Mitglied type. Damit ist die Zeile 7 nicht gültig. Das ist aber kein Fehler, sondern führt nur dazu, dass für diesen Typ kein Template instanziiert werden kann.
Die Regel in C++ dazu lautet: Wenn das Substituieren des Template-Parameters durch ein Template-Argument bei einem Funktions-Template fehlschlägt, wird die Templatespezialisierung für den Typ des Template-Arguments aus der Menge aller möglichen Templatespezialisierungen ausgeschlossen. Für diese längliche Regel hat sich das Akronym SFINAE (Substitution Failure Is Not An Error) etabliert.
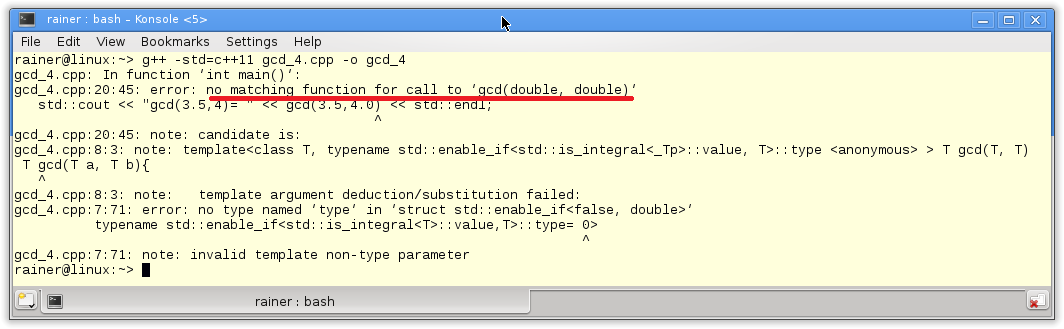
Die Ausgabe des Programms zeigt, das für den Datentyp double keine Templatespezialisierung zur Verfügung steht.
Wie geht's weiter?
Im nächsten Artikel wird es systematischer. Die Type-Traits Bibliothek bietet einen reichen Fundus an Funktionen. Sie erlaubt Typabfragen, -vergleiche und -modifikationen zu Compilezeit. Wie das ganze funktioniert und welche Funktion die Type-Traits Bibliothek zur Verfügung stellt um Typeigenschaften abzufragen, das stellt der nächsten Artikel vor.

 Go to Leanpub/cpplibrary "What every professional C++ programmer should know about the C++ standard library". Hole dir dein E-Book. Unterstütze meinen Blog.
Go to Leanpub/cpplibrary "What every professional C++ programmer should know about the C++ standard library". Hole dir dein E-Book. Unterstütze meinen Blog.






Weiterlesen...