Inhaltsverzeichnis[Anzeigen]

 

Expression Templates

Expression Templates
is a C++ template metaprogramming technique in which templates are used to represent part of an expression. (http://en.wikipedia.org/wiki/Expression_templates)
Die Technik wurde unabhängig von Todd Veldhuizen und David Vandevoorde entwickelt.

Domain-Specific-Embedded-Language (DSEL)

DSEL
Sprache, die auf eine spezielle Domäne ausgerichtet ist und darüber hinaus in der Gastgebersprache, in diesem Falle C++, eingebettet ist.

Charkteristiken

Ermöglicht es mit Hilfe von Template Metaprogramming und Operatur Überladung
  • in der Universalsprache C++ eine mächtige, spezielle Subsprachen für besondere Anwendungsbereiche zu definieren
  • , das sowohl die Gast- wie auch die Gastgebersprache der C++ Syntax genügen (vgl. YACC, antlr, flex oder auch make als Domain-Specific-Languages)

Klassischer Anwendungsfall: Rechnen mit Matrizen

Naiver Ansatz: Operator Überladung

Mittels Operator Überladung lassen sich Vektoroperationen wie Vektor x = b*c + d*esehr natürlich ausdrücken. Die Addition und Multiplikation zweier Vektoren ist schnell implementiert.

Das Hauptprogramm


#include <chrono>
#include <iostream>

#include "vekUtils.h"
#include "vektor.h"

int main(){
  Vektor<int> b(LENGTH);

  Vektor<int> c(LENGTH);
  Vektor<int> d(LENGTH);

  Vektor<int> e(LENGTH);
  for (size_t i=0; i < LENGTH; ++i){

    b[i]=i;
    c[i]=i+i;

    d[i]=i+i+i;
    e[i]=i+i+i+i;

  }
  auto begin= std::chrono::monotonic_clock::now();

  auto x= b*c + d*e; 
  auto last=  std::chrono::monotonic_clock::now() - begin;

  std::cout <<  "calculating  Vektor<int> x= b*c + d*e; with Vektors of length " 
            << LENGTH << " takes " << std::chrono::duration<double>(last).count() 
            << " seconds" << std::endl;

  showMe(x,10);
  Vektor<double> f(LENGTH);

  Vektor<double> g(LENGTH);
  double val;
  for (size_t i=0; i < LENGTH; ++i){

    val= 0.01*i;
    f[i]=val;

    g[i]=1+val;
  }
  begin= std::chrono::monotonic_clock::now();

  auto y= f*g;
  last=  std::chrono::monotonic_clock::now() - begin;

  std::cout <<  "calculating  Vektor<double> y= f*g; with Vektors of length " 
            << LENGTH << " takes " << 
  std::chrono::duration<double>(last).count() << " seconds" << std::endl;

  showMe(y,10);
  
}

 

Der Vektor


template <typename T>
class Vektor{
  public:

    
  Vektor(size_t s): data(new T[s]),dataSize(s){

    for(size_t i=0; i< size(); ++i) data[i]= T();

  }
  
  ~Vektor(){
    delete[] data;
  }

  
  Vektor& operator= (Vektor<T> const& other){
    if ( &other != this){

      for (size_t i=0; i<size(); ++i){

    data[i]= other.data[i];
      }
    }

    return *this;
  }
    
  T operator[] (size_t i) const{

    return data[i];
  }
  
  T& operator[] (size_t i){

    return data[i];
  }
  
  
  size_t size() const{

    return dataSize; 
  }
  
  private:
   
    T* data;

    size_t dataSize;
};

 

Die Arithmetik


template <typename T>

Vektor<T> operator+ (Vektor<T> const& a, Vektor<T> const& b){

  Vektor<T> res(a.size());
  for (size_t i=0; i < a.size(); ++i){

    res[i]= a[i] + b[i];

  }
  return res;
}

template <typename T>

Vektor<T> operator* (Vektor<T> const& a, Vektor<T> const& b){

  Vektor<T> res(a.size());
  for (size_t i=0; i < a.size(); ++i){

     res[i]= a[i] * b[i];

  }
  return res;
}

 

Das Performanceproblem

Diese naive Technik besitzt gravierende Nachteile arrowbrightDie Operatoren sind gierig. Dies führt zu unnötigen Erzeugen von temporären Vektoren und überflüssigen Lese- und Schreibezugriffen.
  1. der Ausdruck Vektor x = b*c + d*ebenötigt 3 temporäre Vektoren
    1. temp1= b*c
    2. temp2= d*e
    3. temp3= temp1+temp2
    4. x= temp3
  2. statt dem eimaligen Lesen jedes Vektors b,c,d und e und dem einmaligen Schreiben des Ergebnisses in x müssen 3 temporäre Vektoren zusätzlich geschrieben und gelesen werden

Idee: Wende lazy evaluation an

  • rolle den Gesamtausdruck aus, bevor die Operatoren angewandt werden
  • werte den Gesamtausdruck erst bei der Ergebniszuweisung aus
  • wende die Vektoroperation x[i] = b[i]*c[i] + d[i]*e[i] elementweise für jeden Index i aus, sodass weder temporäre Vektoren noch zusätzliche Lese- oder Schreiboperationen notwendig sind

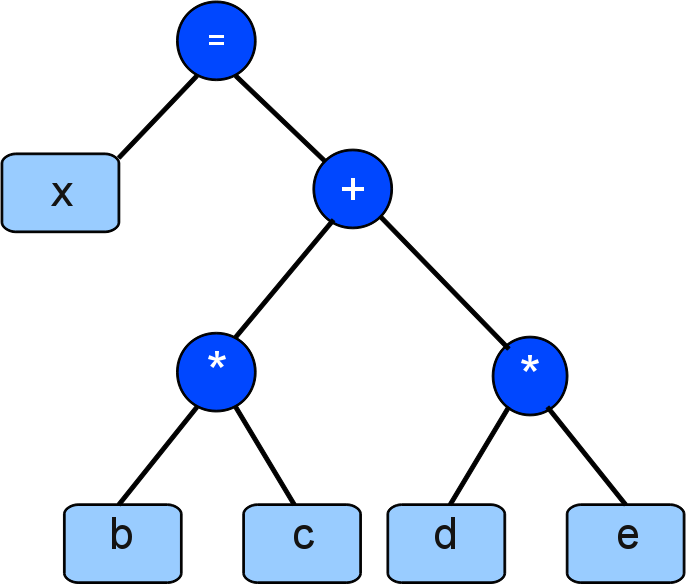
Technik

Zur Compilezeit wird aus den Expression Template ein Parse Tree erzeugt.
  • Parse Tree:
    ParseTree.png

Laufzeitvergleich

Das gleiche Programm zur Vektorarithmethik mit Expression Templates implementiert, bringt einen deutlichenPerformancegewinn. Zur Kontrolle gebe ich jeweils die ersten zehn Werte aus.
  1. klassische Variante 
    calculating  Vektor<int> x= b*c + d*e; with Vektors of length 50000000 takes 5.20741 seconds
    0 14 56 126 224 350 504 686 896 1134 ...
    calculating  Vektor<double> y= f*g; with Vektors of length 50000000 takes 9.72478 seconds
    0 0.0101 0.0204 0.0309 0.0416 0.0525 0.0636 0.0749 0.0864 0.0981 ...
  2. Expression Templates Variante (vermutlich schlägt hier lazy evaluation zu) 
    calculating  Vektor<int> x= b*c + d*e; with Vektors of length 50000000 takes 1e-06 seconds
    0 14 56 126 224 350 504 686 896 1134 ...
    calculating  Vektor<double> y= f*g; with Vektors of length 50000000 takes 1e-06 seconds
    0 0.0101 0.0204 0.0309 0.0416 0.0525 0.0636 0.0749 0.0864 0.0981 ...
Fazit
  1. Vermeidung temporärer Variablen
    • die reine Arithmetik x= b*c + d*e ist natürlich deutlich schneller, da weder temporäre Vektoren allokiert/deallokiert noch unnötige Lese- und Schreiboperation auf den temporären Vektoren notwendig sind
  2. Compilezeit
    • die beiden Programme besitzten ein ähnliches Compilzeitverhalten 
      grimm@laiard ExpressionTemplates $ time g++ -std=c++0x -o vektor vektor.cpp

      real    0m0.373s
      user    0m0.312s
      sys     0m0.056s
      grimm@laiard ExpressionTemplates $ time g++ -std=c++0x -o vektorExpression vektorExpression.cpp

      real    0m0.381s
      user    0m0.320s
      sys     0m0.052s
  3. Laufzeitverhalten
    • die optimierte Arithmetik wirkt sich natürlich auch auf das Laufzeitverhalten des Programmes aus 
      grimm@laiard ExpressionTemplates $ time vektor
      calculating  Vektor<int> x= b*c + d*e; with Vektors of length 50000000 takes 4.35834 seconds
      0 14 56 126 224 350 504 686 896 1134 ...
      calculating  Vektor<double> y= f*g; with Vektors of length 50000000 takes 11.7362 seconds
      0 0.0101 0.0204 0.0309 0.0416 0.0525 0.0636 0.0749 0.0864 0.0981 ...

      real    0m48.025s
      user    0m8.877s
      sys     0m2.120s
      grimm@laiard ExpressionTemplates $ time vektorExpression
      calculating  Vektor<int> x= b*c + d*e; with Vektors of length 50000000 takes 0 seconds
      0 14 56 126 224 350 504 686 896 1134 ...
      calculating  Vektor<double> y= f*g; with Vektors of length 50000000 takes 1e-06 seconds
      0 0.0101 0.0204 0.0309 0.0416 0.0525 0.0636 0.0749 0.0864 0.0981 ...

      real    0m5.349s
      user    0m3.612s
      sys     0m1.044s
Die Vektoroperationen mit Expression Templates sind um den Faktor 9 schneller.

Expression Templates

Weder die Anwendung der Arithemtik im Hauptprogramm noch der Vektor selber unterscheiden sich wesentlich. Lediglich die Vektorarithmetik verändert sich entscheidend.

Das Hauptprogramm

Das Hauptprogramm, das die Expression Templates anwendet, unterscheidet sich nicht vom dem klassischen Ansatz. 


#include <chrono>
#include <iostream>
#include "vekUtils.h"
#include "vektorExpression.h"

int main(){
  VektorExpression<int> b(LENGTH);
  VektorExpression<int> c(LENGTH);

  VektorExpression<int> d(LENGTH);
  VektorExpression<int> e(LENGTH); 
  for (size_t i=0; i<LENGTH; ++i){

    b[i]=i;
    c[i]=i+i;

    d[i]=i+i+i;
    e[i]=i+i+i+i;

  }
  auto begin= std::chrono::monotonic_clock::now();

  auto x= b*c + d*e; 
  auto last=  std::chrono::monotonic_clock::now() - begin;

  std::cout <<  "calculating  Vektor<int> x= b*c + d*e; with Vektors of length " 
            << LENGTH << "takes " << std::chrono::duration<double>(last).count() 
            << " seconds" << std::endl;

  showMe(x,10);
  VektorExpression<double> f(LENGTH);

  VektorExpression<double> g(LENGTH);  
  double val;
  for (size_t i=0; i < LENGTH; ++i){

    val= 0.01*i;
    f[i]=val;

    g[i]=1+val;
  }
  begin= std::chrono::monotonic_clock::now();

  auto y= f*g;
  last=  std::chrono::monotonic_clock::now() - begin;

  std::cout <<  "calculating  Vektor<double> y= f*g; with Vektors of length " 
            << LENGTH << " takes " << std::chrono::duration<double>(last).count() 
            << " seconds" << std::endl;

  showMe(y,10);

 

  • durch auto y= f*g nehme ich das Expression Template an, den der exakte Typ ist nicht einfach zu bestimmen

Der Vektor


template <typename T>
class VektorExpression{

  public:
  
  typedef T ElementType; 
  
  VektorExpression(size_t s): data(new T[s]),dataSize(s){

    for(size_t i=0; i< size(); ++i) data[i]= T();

  }
  
  ~VektorExpression(){
    delete[] data;
  }

  
  template <typename Expression>
  VektorExpression<T>& operator= (Expression const& other){

    if ( &other != this){
      for (size_t i=0; i<size(); ++i){

    data[i]= other[i];
      }
    }

    return *this;
  }
  
  T operator[] (size_t i) const{

    return data[i];
  }
  
  T& operator[] (size_t i){

    return data[i];
  }
  
  size_t size() const{

    return dataSize; 
  }
  
  private:
    
    T* data;

    size_t dataSize;

 

  • der einzige Unterschied zwischen den Typen Vektor und VektorExpression ist, das VektorExpression einen parametrisierten Zuweisungsoperator besitzt, der eine Expression annehmen kann

Die Arithmetik



/* the expression tree node */
/* define the primary template*/
template <typename Left, typename Operation, typename Right>

struct Expression{
  Expression( Left const& l, Right const& r): left(l), right(r) {}

  
  typedef typename Operation::ElementType ElementType; 
  
  ElementType operator[](size_t index) const{

    return Operation::apply(left[index],right[index]);
  }

  
  Left const& left;
  Right const& right;
};

/* the forward declaration of the arithmetic functions*/
template<typename ET>  struct Plus;
template<typename ET>  struct Mult; 


// addition of the expressions
template <typename Left,typename Right>
Expression<Left,Plus<typename Left::ElementType>,Right> 

operator+ (Left const& l, Right const& r){

  return Expression<Left,Plus<typename Left::ElementType>,Right>(l,r);

}

// multiplication of the expressions
template <typename Left,typename Right>
Expression<Left,Mult<typename Left::ElementType>,Right> 

operator* (Left const& l, Right const& r){

  return Expression<Left,Mult<typename Left::ElementType>,Right>(l,r);

}

// elementwise addition
template <typename ET>
struct Plus{
  typedef ET ElementType;

  static ElementType apply(ElementType l,ElementType r){
    return l+r;

  }
};

// elementwise multiplication
template <typename ET>
struct Mult{

  typedef ET ElementType;
  static ElementType apply(ElementType l, ElementType r){

    return l*r;
  }
};

 

Was geschieht nun zur Compilezeit mit dem Ausdruck x= b*c + d*e:
  1. der Ausdruck b*c + d*ewird ausgerollt
    1. die Multiplikationen werden angewandt operator operator * 
      Expression<VektorExpression<double>,Mult<double>,VektorExpression<double> >
    2. die Addition wird auf die Teilausdrücke angewandt operator + 
      Expression< Expression<VektorExpression<double>,Mult<double>,VektorExpression<double> > ,
                 Plus<double>,
      Expression<VektorExpression<double>,Mult<double>,VektorExpression<double> >  >
  2. der Gesamtaudruck wird zugewiesen operator = und stösst die Berechnung der Werte über den Indexoperator operator []an
    • für jeden Index des Vektors wird Operation::apply(left[index],right[index]);ausgerollt und ausgerechnet 
      x[index]= b[index]*c[index] + d[index]*e[index]
Der Datentyp der VektorExpression wird über Plus<typename Left::ElementType> automatisch an die Plus und MultFunktion durchgereicht. Der linke Operand bestimmt das Ergebnis der Operation.

Anwendungen

Blitz++

  • von Todd L. Veldhuizen entwickelt
  • die numerische Bibliothek Blitz++ verbindet hoch performante Berechnung von Matrizen und Vektoren mit der komfortablen Ausdrucksweise von Operator Überladung in C++
Blitz++is a C++ class library for scientific computing which provides performance on par with Fortran 77/90.

Beispiel

Arrayausdrücke
Die arithmetische Operation über Arrays 

#include <iostream>
#include <blitz/array.h>

using namespace blitz;

int main()
{
    Array<float,2> A(3,3), B(3,3), C(3,3);

    A = 1, 0, 0,
        2, 2, 2,

        1, 0, 0;

    B = 0, 0, 7,

        0, 8, 0,
        9, 9, 9;

    C = A + B;

    std::cout << "A = " << A << std::endl
         << "B = " << B << std::endl
         << "C = " << C << std::endl;

    return 0;
}

 

ergibt die folgende Ausgabe 
A = 3 x 3

[         1         0         0
          2         2         2
          1         0         0 ]

B = 3 x 3
[         0         0         7
          0         8         0
          9         9         9 ]

C = 3 x 3
[         1         0         7
          2        10         2
         10         9         9 ]
Vektorausdrücke
Das einführende Beispiel zu Expression Templates lässt sich natürlich auch in Blitz formulieren. 

include <chrono>
#include <iostream>
#include "../vekUtils.h"
#include <blitz/array.h>

using namespace blitz;

int main(){
  Array<int,1> b(LENGTH);

  Array<int,1> c(LENGTH);
  Array<int,1> d (LENGTH);

  Array<int,1> e(LENGTH);
  Array<int,1> x(LENGTH);

  for (int i=0; i<LENGTH; ++i){

    b(i)=i; 
    c(i)=i+i;

    d(i)=i+i+i;
    e(i)=i+i+i+i;

  }
  auto begin= std::chrono::monotonic_clock::now();

  x= b*c + d*e; 
  auto last=  std::chrono::monotonic_clock::now() - begin;

  std::cout <<  "calculating  Vektor<int> x= b*c + d*e; with Vektors of length " 
            << LENGTH << " takes " << std::chrono::duration<double>(last).count() 
            << " seconds" << std::endl;

  std::cout << x(Range(0,9)) << std::endl;

  Array<double,1> f(LENGTH);
  Array<double,1> g(LENGTH); 
  Array<double,1> y(LENGTH);

  double val;
  for (int i=0; i < LENGTH; ++i){

    val= 0.01*i;
    f(i)=val;

    g(i)=1+val;
  }
  begin= std::chrono::monotonic_clock::now();

  y= f*g;
  last=  std::chrono::monotonic_clock::now() - begin;

  std::cout <<  "calculating  Vektor<double> y= f*g; with Vektors of length " 
            << LENGTH << " takes " << std::chrono::duration<double>(last).count() 
            << " seconds" << std::endl;

  std::cout << y(Range(0,9)) << std::endl;

}

 

Das Laufzeitverhalten der drei Implementierung:
  1. klassische OO Ansatz 
    calculating  Vektor<int> x= b*c + d*e; with Vektors of length 10000000 takes 0.772866 seconds
    0 14 56 126 224 350 504 686 896 1134 ...
    calculating  Vektor<double> y= f*g; with Vektors of length 10000000 takes 0.356094 seconds
    0 0.0101 0.0204 0.0309 0.0416 0.0525 0.0636 0.0749 0.0864 0.0981 ...

    real    0m2.099s
    user    0m1.676s
    sys     0m0.368s
  2. Expression Template Implementierung 
    calculating  Vektor<int> x= b*c + d*e; with Vektors of length 10000000 takes 1e-06 seconds
    0 14 56 126 224 350 504 686 896 1134 ...
    calculating  Vektor<double> y= f*g; with Vektors of length 10000000 takes 0 seconds
    0 0.0101 0.0204 0.0309 0.0416 0.0525 0.0636 0.0749 0.0864 0.0981 ...

    real    0m0.952s
    user    0m0.740s
    sys     0m0.204s
  3. Blitz++ 
    calculating  Vektor<int> x= b*c + d*e; with Vektors of length 10000000 takes 0.056804 seconds
    10
     [         0        14        56       126       224       350       504
            686       896      1134  ]
    calculating  Vektor<double> y= f*g; with Vektors of length 10000000 takes 0.081442 seconds
    10
     [         0    0.0101    0.0204    0.0309    0.0416    0.0525    0.0636
         0.0749    0.0864    0.0981  ]

    real    0m0.483s
    user    0m0.208s
    sys     0m0.268s
Jede Applikation ist ca. um den Faktor 2 schneller.

Hauptfeatures Array

  • über Elementtyp, Dimension und Speicherlayout (C versus Fortran) parametrisierbar
  • unterstützt
    • Indexzugriff, Slicing und Unterarrays
    • natürliche Arithmetik mit Expression Templates
    • Reduktion auf einen einzigen Ausgabewert (min, max, mean, count ...)

Optimierungen

Expression Templates
Durch das Instanziieren der Templates zur Compilezeit und der damit verbundenen Evaluierung der Templateausdrücke, werden temporäre Variablen und Speicherzugriffe auf das notwenigste reduziert.
Darüber hinaus können in Blitz++ noch weitergehende Optimierungen angewandt werden, da die arithmetischen Ausdrücke als ganzes im Parse-Tree vorliegen, bevor sie evaluiert werden.
Vertauschen von Schleifen (loop interchange)

for (i = 0; i < N1; ++i){  
  for (j = 0; j < N2; ++j){   
    a[i][j]= b[i][j]*c[i][j];  
  }  

}

 


Für den Prozessor ist es optimal, wenn die Speicherlayout so ist, das die Elemente mit Laufindex k direkt nebeneinander im Speicher liegen. In diesem Fall liest er die eingelesen Cache-Line vom Hauptspeicher direkt verarbeiten. Diese Schleifenstruktur entspricht dem Speicherlayout von C-Programmen, aber nicht den Fortran Programmen. Bei der Loop interchange Optimierung werden die Indizes vertauscht um den Speicherzugriff für den Prozessor zu optimieren. Dies kann einfach durch die Vertauschung der Spalten erreicht werden. 


for (j = 0; j < N2; ++j){  
  for (i = 0; i < N1; ++i){   
    a[i][j]= b[i][j]*c[i][j];  
  }  

}

 

Extrahieren der Schrittweitenberechnungen (Hoisting stride calculations)
In einem Ausdruck der Form 

for (int i = 0; i < 100; ++i) {

  // use array[i];
}

 

muss der Arrayzugriff array[i] in jeder Iteration durch ((byte*)array)[sizeof(T)*index]ermittelt werden. Das ist teuer. Durch 

int stride = sizeof(T);
for (int i = 0; i < 100; i += stride) {

  // use array[i];
  
}

 

wird die Multplikation durch eine Addition ersetzt und die Schrittweite im vorraus berechnet. Dadurch ist der Arrayzugriff array[i] deutlich einfacher: ((byte *)array)[i].
Innere Schleifen auflösen (Collapsing inner loops)
Blitz löst die innere Schleife auf, falls sie hinreichend klein ist.
Teilweise auflösen der inneren Spalte (Partial loop unrolling)
Ist die Schleife zu gross, bietet sich das teilweie auflösen der Schleife an.
Aus 

for (i=0; i<60; i++) a[i] = a[i] * b + c;

 

wird somit 

for (i=0; i<60;) {

  a[i++] = a[i] * b + c;

  a[i++] = a[i] * b + c;

  a[i++] = a[i] * b + c;

  a[i++] = a[i] * b + c;

  a[i++] = a[i] * b + c;

  a[i++] = a[i] * b + c;

}

 

Schleifenblöcke (Loop tiling, Loop blocking)
Um mögliche cache misses zu vermeiden und die cache line optimal auszunützen, kann die Iteration über ein 2-dimensionalen Raum in viele Iterationen über kleine Blöcke aufgebrochen werden.
Aus 

for (i=0; i<N; i++){

  for (j=0; j<N; j++){

    c[i] = c[i]+ a[i,j]*b[j];

  }
}

 

wird 

for (i=0; i<N; i+=2){

  for (j=0; j<N; j+=2){

    for (ii=i; ii<min(i+2,N); ii++){

      for (jj=j; jj<min(j+2,N); jj++){

        c[ii] =c[ii]+ a[ii,jj]*b[jj];

      }
    }
  }
}

 

Spirit

Das Spirit Parser Framework als Teile der Boost Bibliotheken ist ein objektorientierter, rekursiv absteigender Parsergenerator, der mittels Templatemetaprogrammierung und insbesondere Expression Templates implementiert worden ist. Damit lässt sich ein Parser als DSEL direkt in C++ formulieren. Dieser Parser versteht die http://de.wikipedia.org/wiki/Erweiterte_Backus-Naur-Form, mit deren Hilfe eine kontextfreie Grammatikformuliert werden kann.

Module

Das Parser Framework besteht bietet neben dem Parser noch einen Lexer und einen Ausgabe Erzeuger.
  • Spirit Struktur:
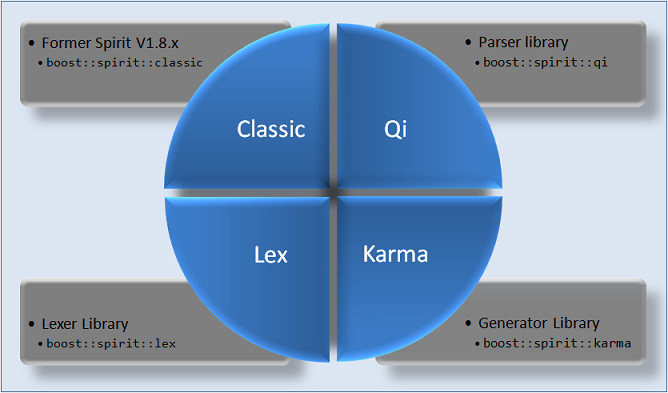
    spiritstructure.png
  • Spirit.Classic: Entspricht Boost Spirit 1.8.x.
  • Spirit.Qi: Rekursive absteigende Parserbibliothek
  • Spirit.Lex: Lexikalischer Analysator
  • Spirit.Karma: Ausgaben Erzeuger

Syntax

SyntaxBedeutung
x >> y x gefolgt von y
*x x null oder mindestens ein Mal
x | y x oder y
+x x mindestens ein Mal
!x x null oder ein Mal
x & y x und y
x - y x aber nicht y
x ^ y x oder y aber nicht beide zusammen
( x ) Angabe der Prioriät
x % y eine oder mehrere Wiederholungen von x, getrennt durch y
~x alles außer x
x[FunktionsAusdruck] wende den Funktionsausdruck auf x an

EBNF versus Spirit

Das Beispiel für eine Grammatik ist ein Calculator.
EBNF
group       ::= '(' expression ')'

factor      ::= integer | group
term        ::= factor (('*' factor) | ('/' factor))*
expression  ::= term (('+' term) | ('-' term))*
Spirit

group       = '(' >> expression >> ')';

factor      = integer | group;
term        = factor >> *(('*' >> factor) | ('/' >> factor));

expression  = term >> *(('+' >> term) | ('-' >> term));

 

Die Unterschiede sind den Regeln von C++ geschuldet. Dies sind im wesentlichen die Operator Überladung Regeln, die auf äusserster Ebene angewandt werden.
  • ;: '(' >> expression >> ')';
    der Strichpunkt erklärt ein Statement in C++
  • *x: *(('+' >> term) | ('-' >> term))
    der Stern muss vor dem Ausdruck stehen
  • >>: '+' >> term
    der Shift-Operator erklärt die Sequenz von Ausdrücken

Beispiel: Anzahl der Wörter in einer Datei


#include <boost/spirit/include/lex_lexertl.hpp>

#include <boost/spirit/include/qi.hpp>

#include <fstream>
#include <iostream>
#include <map>

#include <string>

std::string getLineByLine(char const* inFile) {

  std::string buffer;
  std::string line;
  std::ifstream inStream(inFile);

  if (!inStream.is_open()) {
    std::cerr << "Couldn't open file: " << inFile << std::endl;

    exit(-1);
  }
  while(std::getline(inStream,line))

  buffer += line;
  return buffer;
}

struct allWords{

  void operator()(const std::string& key, boost::spirit::qi::unused_type, 
                  boost::spirit::qi::unused_type) const{

    ++allWords_[key];
  }
  const std::map<std::string,int>& getAllWords() const {

    return allWords_;
  }
  private:
    static std::map<std::string,int> allWords_;  

};
std::map<std::string,int> allWords::allWords_;

template <typename Lexer> 
struct wordCountTokens : boost::spirit::lex::lexer<Lexer>{

  wordCountTokens(){
    this->self.add_pattern("WORD", "[^ \t\n]+");

    this->self.add_pattern("SPACE","[ \t\n]+");
    word = "{WORD}";

    space= "{SPACE}";
    this->self.add(word)

          (space);        
  }
  boost::spirit::lex::token_def<std::string> word;

  boost::spirit::lex::token_def<std::string> space;
};

template <typename Iterator>
struct wordCountGrammar : boost::spirit::qi::grammar<Iterator>{

  template <typename TokenDef> 
  wordCountGrammar(TokenDef const& tok): wordCountGrammar::base_type(start){

    start =  *(tok.word[allWords()]
              |tok.space);

    }
  boost::spirit::qi::rule<Iterator> start;
};

int main(int argc, char **argv ){

  typedef boost::spirit::lex::lexertl::token<char const*, 
          boost::mpl::vector<std::string> > tokenType;

  typedef boost::spirit::lex::lexertl::lexer<tokenType> lexerType;

  typedef wordCountTokens<lexerType>::iterator_type iteratorType;
  
  wordCountTokens<lexerType> myLexer;           
  wordCountGrammar<iteratorType> myGrammar(myLexer); 

  std::string myString= getLineByLine(argv[1]);

  char const* first = myString.c_str();
  char const* last = &first[myString.size()];

  
  bool r = boost::spirit::lex::tokenize_and_parse(first, last, myLexer, myGrammar);

  allWords myWordCount;
  const std::map<std::string,int> myWords= myWordCount.getAllWords();

  std::map<std::string,int>::const_iterator  pos;
  if (r) { 
    std::cout << "{";

    for ( pos= myWords.begin(); pos != myWords.end(); ++pos){

      std::cout << "(" << pos->first << "," << pos->second << ")";

    }
    std::cout << "}" << std::endl;
  }

  else {
    std::string rest(first, last);

    std::cerr << "Parsing failed\n" << "stopped at: \""  << rest << "\"\n";

  }
  return 0;
}

 

  • damit lassen sich die Anzahlt der Wörter in einer Datei zählen 
    grimm@laiard wordCount $ ./wordCount /etc/protocols
    {(",2)("A,2)("Aggregation,1)("Assigning,1)("CFTP",,1)("DDN,1)("Datagram,1)("Dissimilar,1)
    ("Encapsulating,1)("EtherIP:,1)("Experimental,1)("Gateway,1)("Host,1)("IP,3)("IP#,1)
    ("ISO,1)("Internet,4)("Internet#,1)("Mobility,1)("Multiplexing,1)
    ("NETBLT:,1)("Next,1)("PUP:,1)("Protocol",,1)("Reliable,1)("ST,1)("STUB",1)
    .
    .
    .
    (there,1)(this,1)(to,1)(updated,1)(use,1)(using,1)(uti,1)(version,2)(with,1)(within,2)(xtp,1)}
  • Anmerkungen:
    • std::string getLineByLine(char const* inFile) liest die ganze Datei ein und gibt sie als String zurück, nachdem die Zeilenendzeichen entfernt wurden
    • struct allWords inkrementiert für jeden neuen Schlüssel in ++allWords_[key] den Zähler
    • struct wordCountTokensdefiniert die Tokens, die mein Lexer an den Parser zurückgibt
      • this->self.add_pattern("WORD", "[^ \t\n]+") beschreibt ein Word
      • this->self.add_pattern("SPACE","[ \t\n]+") beschreibt einen Spaceausdruck
    • struct wordCountGrammar ist der Parser, der eine Regel kennt: *(tok.word[allWords()] | tok.space)
      • tok.word[allWords()] ist die semantische Aktion für das gefundene Wort
      • tok.space für die Leerzeichen existiert keine semantische Aktion
    • boost::spirit::lex::tokenize_and_parse(first, last, myLexer, myGrammar) verbindet den Lexer mit dem Parser und wertet den Tokenstream von [first,last[ aus
    • myWordCount.getAllWords() gibt das Ergebnis der Parserlaufs als Map zurück

Einführung

Eine sehr gute Einführung in das neue Spirt.

Platz, Stelle, Stätte, Baugelände, Gelände, Baustelle, Grundstück, Standort, legen, anlegen [site]

Mentoring

Stay Informed about my Mentoring

 

Bücher

Interaktive Kurse

Artikel

Rezensionen

Vorträge

Videos

Tutorial

Besucher

Heute 923

Gestern 3357

Woche 12486

Monat 39803

Insgesamt 3892517

Aktuell sind 35 Gäste und keine Mitglieder online

Kubik-Rubik Joomla! Extensions

Kontakt

Abonniere den Newsletter (+ pdf Päckchen)

Kategorien

Alle Tags

Beiträge-Archiv

Sourcecode

Neuste Kommentare